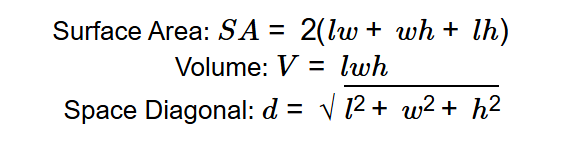Introduction

The Cuboid Surface Area Calculator is a powerful tool designed to compute the total surface area, volume, and space diagonal of a cuboid (rectangular prism) based on its length (\( l \)), width (\( w \)), and height (\( h \)). This calculator is essential for applications requiring precise geometric measurements, such as material estimation, structural design, and educational purposes.

Why is the “Cuboid Surface Area Calculator” Important?

Accurate cuboid calculations are vital for:

• Material Planning: Determining the amount of material (e.g., paint, wrapping) needed to cover a cuboid’s surfaces.
• Design Optimization: Ensuring efficient design of cuboidal structures, such as rooms, containers, or packaging.
• Educational Purposes: Enhancing understanding of cuboid geometry in mathematics and engineering education.
• Engineering Precision: Providing accurate measurements for manufacturing and construction projects involving cuboidal shapes.

How the “Cuboid Surface Area Calculator” Works

The calculator processes user inputs—length, width, and height with their respective units—to calculate the cuboid’s surface area, volume, and space diagonal. It converts inputs to meters for consistent computations, applies geometric formulas, and provides results in multiple units (cm, m, in, ft for lengths; cm², m², mm², in², ft² for area; cm³, m³, in³, ft³ for volume) to suit various applications.

Formulas Used in the “Cuboid Surface Area Calculator”

The calculator employs the following equations:

• Surface Area: \( SA = 2(lw + wh + lh) \)
• Volume: \( V = lwh \)
• Space Diagonal: \( d = \sqrt{l^2 + w^2 + h^2} \)

Where:

• \( l \): Length of the cuboid (in mm, cm, m, in, ft).
• \( w \): Width of the cuboid (in mm, cm, m, in, ft).
• \( h \): Height of the cuboid (in mm, cm, m, in, ft).
• \( SA \): Total surface area of the cuboid (in cm², m², mm², in², ft²).
• \( V \): Volume of the cuboid (in cm³, m³, in³, ft³).
• \( d \): Space diagonal, from one corner to the opposite corner (in cm, m, in, ft).

Step-by-Step Breakdown of the Formulas

The calculation process involves:

1. Input Dimensions: Enter the length (\( l \)), width (\( w \)), and height (\( h \)) of the cuboid, selecting units (mm, cm, m, in, ft).
2. Validate Inputs: Ensure \( l \), \( w \), and \( h \) are positive values.
3. Convert Units: Convert length, width, and height to meters using conversion factors (e.g., 1 mm = 0.001 m).
4. Calculate Surface Area: Compute the surface area using \( SA = 2(lw + wh + lh) \).
5. Calculate Volume: Compute the volume using \( V = lwh \).
6. Calculate Space Diagonal: Compute the space diagonal using \( d = \sqrt{l^2 + w^2 + h^2} \).
7. Convert Results: Convert surface area to cm², m², mm², in², ft²; volume to cm³, m³, in³, ft³; diagonal to cm, m, in, ft.
8. Format Results: Display results with three decimal places for precision.

Example Calculation

6.1. Input Values

• Length (\( l \)): 2 m
• Width (\( w \)): 3 m
• Height (\( h \)): 4 m

6.2. Calculation Steps

1. Surface Area: \( SA = 2(2 \times 3 + 3 \times 4 + 2 \times 4) = 2(6 + 12 + 8) = 2 \times 26 = 52 \, \text{m}^2 \)
2. Volume: \( V = 2 \times 3 \times 4 = 24 \, \text{m}^3 \)
3. Space Diagonal: \( d = \sqrt{2^2 + 3^2 + 4^2} = \sqrt{4 + 9 + 16} = \sqrt{29} \approx 5.385 \, \text{m} \)
4. Convert Units:
   • Surface Area: \( 52 \times 10000 = 520000 \, \text{cm}^2 \), \( 52 \times 1000000 = 52000000 \, \text{mm}^2 \), \( 52 \times 1550 = 80600 \, \text{in}^2 \), \( 52 \times 10.7639 \approx 559.723 \, \text{ft}^2 \)
   • Volume: \( 24 \times 1000000 = 24000000 \, \text{cm}^3 \), \( 24 \div (0.0254)^3 \approx 1464568.245 \, \text{in}^3 \), \( 24 \div (0.3048)^3 \approx 847.552 \, \text{ft}^3 \)
   • Space Diagonal: \( 5.385 \times 100 = 538.516 \, \text{cm} \), \( 5.385 \div 0.0254 \approx 211.811 \, \text{in} \), \( 5.385 \div 0.3048 \approx 17.667 \, \text{ft} \)
5. Results:
   • Surface Area: 520000.000 cm², 52.000 m², 52000000.000 mm², 80600.000 in², 559.723 ft²
   • Volume: 24000000.000 cm³, 24.000 m³, 1464568.245 in³, 847.552 ft³
   • Space Diagonal: 538.516 cm, 5.385 m, 211.811 in, 17.667 ft

Conclusion

The Cuboid Surface Area Calculator simplifies the computation of a cuboid’s surface area, volume, and space diagonal, providing results in multiple units for diverse applications. Its accuracy and user-friendly interface make it an essential tool for education, engineering, and design.

How to Use the “Cuboid Surface Area Calculator”

8.1. Understanding the Input Fields

• Length (\( l \)): Enter the length of the cuboid and select a unit (mm, cm, m, in, ft).
• Width (\( w \)): Enter the width of the cuboid and select a unit (mm, cm, m, in, ft).
• Height (\( h \)): Enter the height of the cuboid and select a unit (mm, cm, m, in, ft).

8.2. How to Interpret the Results

• Surface Area: The total surface area in cm², m², mm², in², ft² (to 3 decimal places).
• Volume: The volume in cm³, m³, in³, ft³ (to 3 decimal places).
• Space Diagonal (\( d \)): The diagonal across the cuboid in cm, m, in, ft (to 3 decimal places).

Practical Applications & Expert Insights

9.1. Where the “Cuboid Surface Area Calculator” is Used

• Architecture: Designing cuboidal structures like rooms, buildings, or storage units.
• Manufacturing: Calculating material needs for cuboidal containers, packaging, or furniture.
• Education: Teaching geometric concepts of cuboids in mathematics and engineering courses.
• Product Design: Estimating surface area for coating, painting, or wrapping cuboidal objects.

9.2. Real-Life Scenarios

• Construction Project: An architect calculates the surface area of a cuboidal room to determine paint or wallpaper requirements.
• Industrial Production: A manufacturer estimates the material needed for a cuboidal shipping container.
• Classroom Learning: A student verifies cuboid volume and diagonal calculations for a geometry assignment.

9.3. Expert Recommendations

• Precision in Measurements: Ensure accurate length, width, and height inputs, as errors can significantly affect calculations.
• Unit Consistency: Use the same unit for all dimensions to avoid conversion errors.
• Material Allowance: Add 5-10% to the surface area for waste or overlap when planning material purchases.
• Verification: Cross-check results with manual calculations or CAD software for critical applications.

Frequently Asked Questions (FAQs)

10.1. What is the Cuboid Surface Area Calculator?

It’s a tool that calculates the surface area, volume, and space diagonal of a cuboid based on its length, width, and height.

10.2. How is the surface area of a cuboid determined?

The surface area is calculated using \( SA = 2(lw + wh + lh) \), where \( l \), \( w \), and \( h \) are the length, width, and height, respectively.

10.3. Why are multiple units provided for results?

Multiple units (cm, m, in, ft for lengths; cm², m², mm², in², ft² for area; cm³, m³, in³, ft³ for volume) accommodate diverse user needs across regions and industries.

10.4. Can the calculator handle negative or zero inputs?

No, length, width, and height must be positive, as negative or zero values are invalid for a cuboid’s geometry.

10.5. What are the practical applications of cuboid calculations?

They are used in architecture, manufacturing, education, and product design to estimate material requirements and analyze cuboidal structures.

10.6. Where can I find more information on cuboid geometry?

Refer to geometry textbooks, online resources like MathWorld (mathworld.wolfram.com), or consult mathematics educators for detailed cuboid properties.

Cuboid Surface Area Calculator© - All Rights Reserved 2025